Continuity
In its most general form, a function between topological spaces
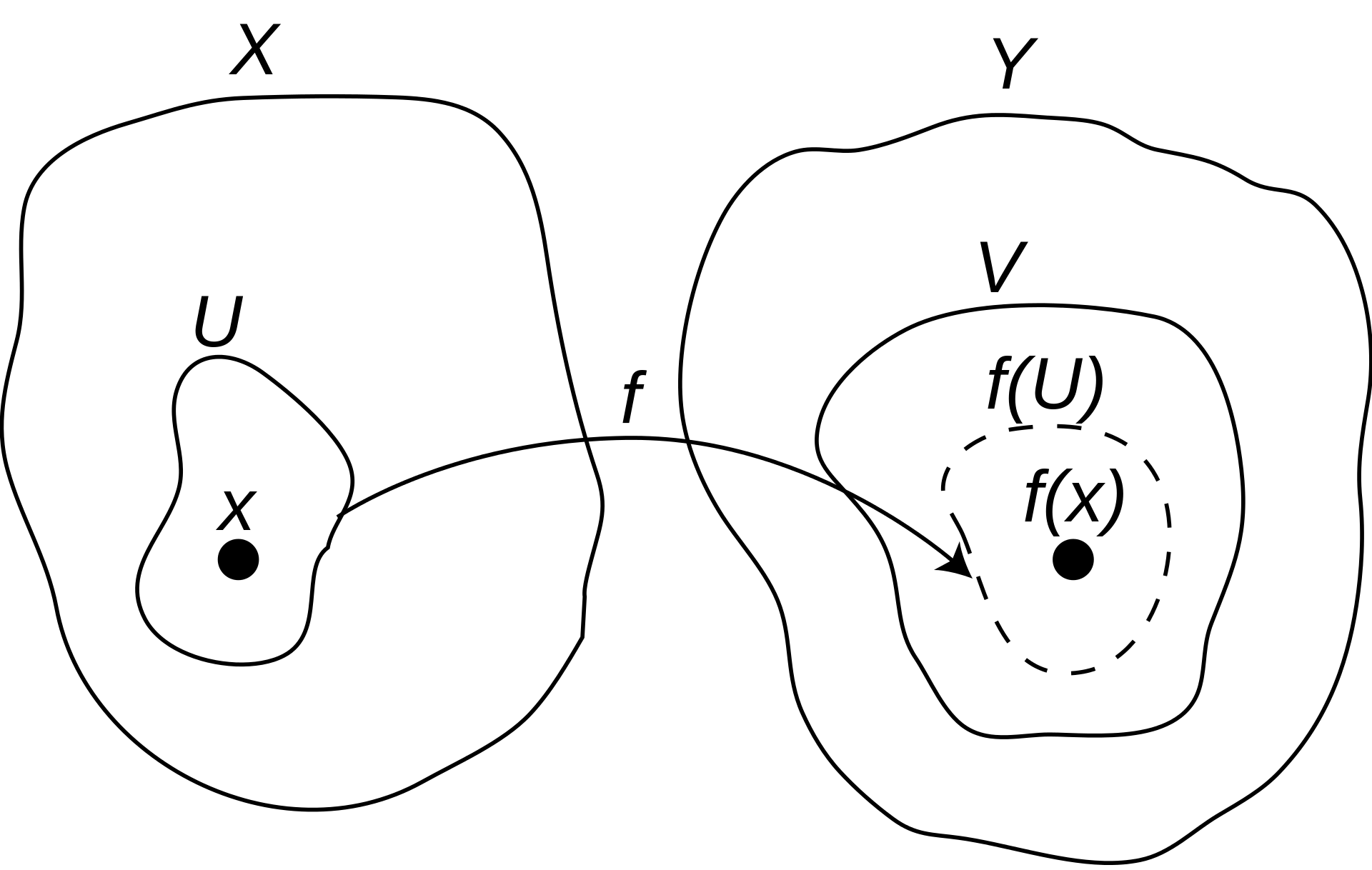
A function is continuous iff. it is continuous at every point in its domain,
or equivalently iff. the preΓ―mage of every open set is open. topology Category of topological spaces has such functions as its morphisms.
We write
Proof of equivalence of open and general neighbourhood pointwise definitions
Let
and ( π , T π ) be topological spaces, and ( π , T Y ) . π : π β π First assume for every open neighbourhood
of π β T π , there exists an open neighbourhood π ( π ) of π β T π , such that π . Given an arbitrary neighbourhood π ( π ) β π of π β² , there exists an open neighbourhood π ( π ) such that π . Thence there exists an open neighbourhood π₯ β π β π β² of π , such that π . Therefore for every neighbourhood π ( π ) β π β π β² of π β² , there exists a neighbourhood π ( π ) of π , such that π . π ( π ) β π β² For the converse, assume for every neighbourhood
of π , there exists a neighbourhood π ( π ) of π β² , such that π . Let π ( π ) β π be an open neighbourhood of π . Then there exists a neighbourhood π ( π ) of π β² such that π . It follows there exists an open neighbourhood π ( π β² ) β π of π β π β² , such that πΆ . Therefore for every open neighbourhood π ( π ) β π of π , there exists an open neighbourhood π ( π ) of π , such that π . π ( π ) β π
Proof of equivalence of pointwise and preΓ―mage definition
Let
and ( π , T π ) be topological spaces, and ( π , T Y ) . π : π β π First assume the preΓ―mage of every open set is open. Let some
, and π β π be an open neighbourhood of π . The preΓ―mage π ( π ) is then an open neighbourhood of π = π β 1 ( π ) , and π (image of preΓ―mage). Therefore, given any π ( π ) = π ( π β 1 ( π ) ) β π and any open neighbourhood π β π of π , there exists an open neighbourhood π ( π ) of π such that π . π ( π ) β π For the converse, assume given any
and any open neighbourhood π β π of π , there exists an open neighbourhood π ( π ) of π such that π . Let π ( π ) β π be an open set. For every π β T π , let π β π β 1 ( π ) be an open neighbourhood of π π such that π . Take the union π ( π π ) β π , which is an open neighbourhood of every π = β π β π β 1 ( π ) π π , whence π β π β 1 ( π ) Since every π β 1 ( π ) β π it follows that π ( π π ) β π , whence π ( π ) β π . Thus π β π β 1 ( π ) is open. Therefore the preΓ―mage of every open set is open. π = π β 1 ( π )
A continuous bijection with a continuous inverse is a Homeomorphism2.
Special cases
In a metric space
If
A function
is continuous at a point π : π β π iff. for every π β π there exists π > 0 such that πΏ > 0 , i.e. π ( π΅ πΏ ( π ) ) β π΅ π ( π ( π ) ) for any π ( π₯ ) β π΅ π ( π ( π ) ) . π₯ β π΅ πΏ ( π )
In metric spaces continuity is equivalent to Sequential continuity,
namely a function is continuous at a point
In the real numbers
Intuitively, a function is continuous if it has no gaps,
i.e. for
and
A function which is differentiable at
Hypernyms include