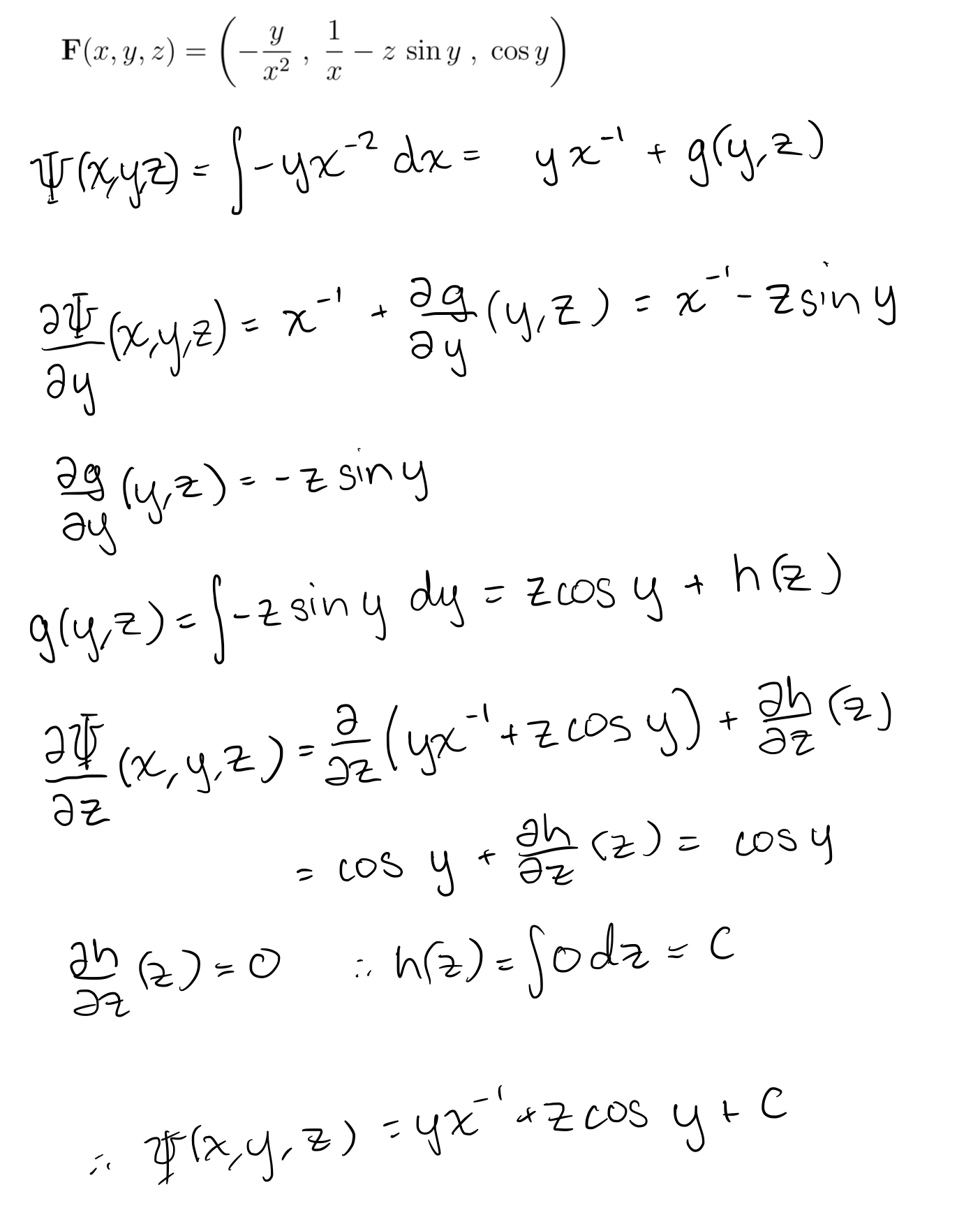Vector field

Conservative vector field

A conservative vector field¹ is a Vector field in which the line integral is path-independent, i.e. only depends on the start and end points. vec

Any conservative vector field may be expressed as the gradient field of some scalar field, called the scalar potential, such that

Deriving a scalar potential

Properties and examples

• The Circulation around any closed path is
• The Curl of any conservative vector field (this follows from Stokes’s theorem). The converse is true on any Simply connected space.
• Fundamental theorem for line integrals may be used

Partially conservative field

As a consequence of Stokes’s theorem, if a simply connected region is irrotational w.r.t. a field (i.e. ), then the vector space is conservative within that region. However any region including a point which is not irrotational is not conservative. In other words, a closed path integral is for any path whose enclosed region is irrotational everywhere.²

Practice problems

Practice problems are mostly for deriving a potential.

• 2023. Advanced Mathematical Methods, p. 28 (§1 problems 12–15)
• 2016. Calculus, pp. 1124–1135 (§16.3 exercises 3–19)
• 2016. Calculus, pp. 1149 (§16.5 exercises 13–18)

---

tidy | sembr | en

Footnotes

1. also called irrotational ↩

2. For an example of this in the two dimensional case, see 2023. Advanced Mathematical Methods, pp. 31–32. ↩