Differential system

Linear differential system

A linear differential system has the form

where is an square matrix.

Solutions

The solution is given by the Matrix exponential, but may alternatively be found by finding the eigenvalues of the matrix , which produces a characteristic polynomial similar to those used to solve Linear second-order differential equations. The example is discussed below.

Unique eigenvalues

If the algebraic multiplicity is the same as the geometric multiplicity for each eigenvalue, take nonzero eigenvectors and . The solution is hence

Complex conjugates

If the eigenvalues are complex conjugates , then Euler’s formula can be used to separate one of the spanning solutions into its real and imaginary parts. This will form a full spanning solution set.

Repeated eigenvalues

If the algebraic multiplicity is the same as the geometric multiplicity for each eigenvalue, the same method as above can be used. However, if the geometric multiplicity is less, the solution will have the form

where is an eigenvector and is a Generalized eigenvector.

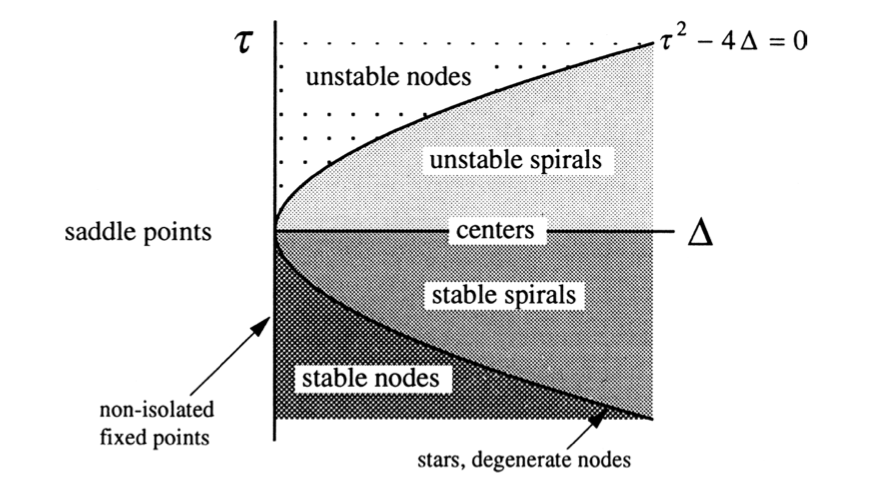
Stability of the origin

In Stability language¹

• If both eigenvalues are negative then the origin is a stable node.
• If both eigenvalues are positive then the origin is an unstable node.
• If the eigenvalues are equal with geometric multiplicity 2 then the origin is a star or symmetric node.
• If an eigenvalue has more algebraic multiplicity than geometric, then it is a degenerate node.
• If some eigenvalues are negative and some are positive, the origin is a saddle point.
• The eigenspace of a negative eigenvalue is a stable manifold, the eigenspace of a positive eigenvalue is an unstable manifold.

Trajectories typically approach the origin tangent to the slow eigendirection.

Practice problems

• 2017. Elementary differential equations and boundary value problems
  • Real-valued: pp. 318–319 (§7.5 problems)
  • Complex-valued: pp. 327–329 (§7.6 problems)
  • Repeated eigenvalues: pp. 343–345 (§7.8 problems)

---

tidy | en | sembr | review

Footnotes

1. 2024. Nonlinear dynamics and chaos: With applications to physics, biology, chemistry, and engineering, §5, pp. 137ff. ↩