Category theory MOC

Yoneda lemma

Let be a locally small category. For every object and every Presheaf we have

where is the Yoneda embedding. Moreover, this bijection is a natural isomorphism in and

where naturality in means for

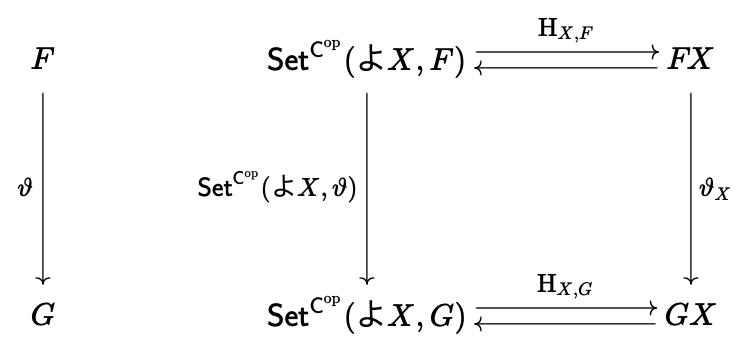
commutes; and naturality in means for

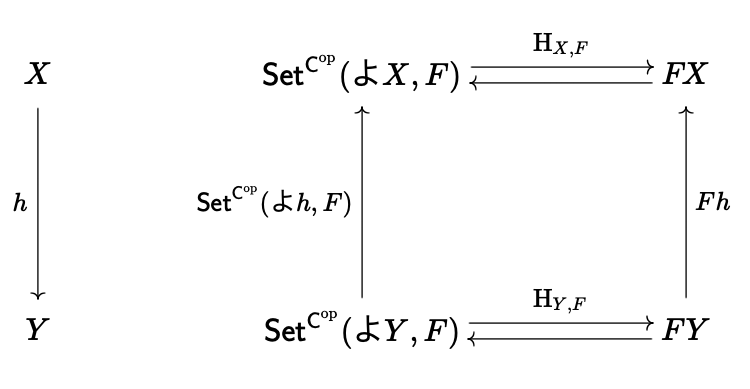
commutes.¹

Proof

For we have . Let .

Conversely, given an , we can define as follows: Given any , we define the component

whose naturality condition is given by the diagram

Now for we have

so is indeed natural.

Now we calculate for . From the above definitions, for we have

but by naturality of

wherefore .

Conversely, for we have

Therefore

defines a bijection for any .

For naturality in , suppose Then for any we have

so the required diagram commutes.

For naturality in , suppose . Then for we have

as required. ^proof

Corollaries

• The “theorem”: The Yoneda embedding is an embedding.

• The Yoneda perspective

• Cayley’s theorem

---

tidy | en | sembr

Footnotes

1. 2010. Category theory, §8.3, pp. 189–192 ↩